Biomechanics of a Pelé’s Bicycle Kick

Marcos Duarte

Sub-atomic particles are traced using the fundamental principles of conservation of Physics; new planets are detected also by means of these principles, embodied in the classical laws of motion stated by the great English physicist Sir Isaac Newton in the seventeenth century.

Two centuries later, the football (soccer) as we know today was created by the English. Nowadays, football is the most popular game in the world with an audience of half of the world population in its 2002 FIFA World Cup. Any movement in nature must obey the Newton's laws of motion, but football adds something on top of that; in its essence, football is a combination of force and speed as well as skill and creativity - a supreme blend of rationality and irrationality.

But some non English players somehow integrated the Newton's laws with creativity in football as nobody else has done; they were leaded by the greatest football player of all times, the Brazilian Edson Arantes do Nascimento, also known as The King and The Artist, but most known by his single name, Pelé.

No other movement in football is as spectacular as the gesture known as the bicycle kick: when a player kicks the ball in mid-air backwards and over his own head. Many players tried it; some of them succeeded but few performed a perfect one. A perfect bicycle kick is a rare event, even in the World Cup it is not guaranteed that one will witness a bicycle kick, but if this happens, the ticket is worth it.

Here we show that the very same laws used to trace particles and to detect planets can be applied to identify a perfect bicycle kick in football. For such, we uncover the subtle details of a bicycle kick performed by the player who had this movement as his signature, Pelé.

See the video of Pelé's bicycle kick here.
Methods

The methods used here belong to an area of study known as Biomechanics. Basically, Biomechanics studies biological systems by means of principles of Mechanics and appropriate experimental methods. The present analysis takes a simple approach to describe the movement under study compared to the actual complexity of human movement; part of this choice is due to methodological limitations but mainly because a simple model works and it is nice to show that sometimes we don't need complicate stuff to understand nature. A detailed analysis of the mechanics of a human movement is very complicate due to the great complexity of the human body: for example, even considering the segments of the human body as rigid bodies, one needs at least 244 independent coordinates to completely characterize the human body position in the tri-dimensional space, i.e., the human body has 244 degrees of freedom (Zatsiorsky, 1998). The physicist Paul Dirac once said that the trick to avoid such difficulty is to divide the problem in two parts, one simple and the other one small. One then solves the simple part exactly and do the best one can with the small part or even neglect it. 

But which is the minimum complexity necessary to have a good and not complex description of the phenomenon? In general, there is no answer to this question and this is a matter of discussion in the field of biomechanics. We can invoke the Ockham's razor principle: 'plurality should not be assumed without necessity', i.e., it's futile to use a complex model if a simple model can explain the phenomenon, or yet in modern English, 'keep it simple, stupid'. But we should have in mind what Einstein said: 'Make the model as simple as possible but not simpler' and never forget that 'for every complex problem, there is a solution that is simple, neat, and wrong' (H.L. Mencken).

Although there are different recordings of a bicycle kick, for a quantitative analysis the video must meet a particular condition: if just one view (from only one camera) is available, to avoid errors of perspective (what frequently happens when judging an offside in football (Oudejans et al., 2000)), this view should be perpendicular to the plane of motion (which then is considered to be a planar movement). One must also know or be able to estimate the relation between the real dimensions of the scene and the image in the video (which is what is going to be analyzed). We were able to find an old video of Pelé satisfying such conditions (see the video). The movement under study is qualitatively similar to other perfect bicycle kicks and the results of the present analysis can be generalized.

For the calculations, the body characteristics mass, center of gravity, and radius of gyration (to calculate the rotational inertia) of each segment were estimated by an anthropometric model (Zatsiorsky, 2002) and from his mass and height, 72 kg and 1.73 m. From each of the 92 video frames, 18 anatomical landmarks of Pelé and the ball position were digitized by commercial software for kinematic analysis called APAS. These digitized coordinates were processed in the mechanical analysis by special software written in MATLAB.
The Bicycle Kick

Ramon Unzaga, from Spain, is credited to have performed the first bicycle kick in 1914. He migrated to Chile and his kick was called the chilena (the term means a Chilean-style kick). The Brazilian player Leônidas da Silva perfected the bicycle kick in the 30’s and 40’s and Pelé made it world famous in the 60’s and 70’s (Galeano, 1999). It takes no more than a second to perform it but this movement is full of details that at first sight we do not realize. In the bicycle kick performed by Pelé that we analyzed, the total movement time is about 0.8 s: he takes 0.3 s to impulse his body and stays in the air for about 0.5 s. The movement phases of this bicycle kick, illustrated in Fig.1a, are:

1. The jumping: Pelé places himself back to the intended direction of the kicked ball and to jump, his center of gravity (CG), defined as a point where the resultant of all the weight forces can be considered acting upon, projects a little behind of his impulse foot. This allows him to gain rotational momentum when he applies force on the ground that passes within a certain distance from the CG to jump like in a back somersault. 
The product between the applied force and the distance from this force to the point of rotation is called torque or moment of a force. The leg that is going to kick the ball is the leg used to propel the body and is the last one to lose contact with the ground. The other leg goes up rotating around the hip while the kicking leg is still in contact with the ground. At movement initiation, his CG is at a height of 0.92 m and it reaches 1.39 m, a vertical displacement of 0.47 m, as shown in Fig.1b.

2. The scissors: Once completely in the air, Pelé, in astonishing synchrony with the ball trajectory, elevates the leg which is going to hit the ball and moves the other leg in the opposite direction; like the movement of a scissors, as can be seen by the angles between the thigh and the trunk for each leg shown in Fig.1c. While the movement is performed, the head is kept in a very stable posture because he must gaze at the ball. 

To facilitate the rotational movement of the kicking leg at the beginning, he bends the knee of this leg, approximating his limbs to the hip, and fully extends this leg just before the kick to hit the ball as high as possible, like the divers do to rotate faster during a dive. The physical property being altered is called the rotational inertia, the property of a body to resist change in its state of angular movement. The rotational inertia is calculated as the product between the body mass and the squared distance from the body to the center of rotation. Decreasing the distances of each segment to the hip joint decreases the total rotational inertia of the lower limb as shown in Fig.1d. In the air, the arms stabilize the body position: the arms are kept away from the trunk in the frontal plane to intentionally increase the body’s rotational inertia in the longitudinal direction to diminish any rotational perturbation in this direction, like a circus acrobat walking on a rope with a balancing beam in the hands.

3. The ball striking: The leg, at high speed, intercepts the ball above the height of a standing person, and changes its movement. Then, for a moment (see the video), it seems as if his body stops in the air and only the legs rotate around the hip. This phenomenon is due to the movement of other segments of the body that move faster than the trunk: although the entire body CG is in a parabolic trajectory, as predicted by the classical laws of motion, the trunk vertical trajectory (trunk CG) actually slows down in its apex, as shown in Fig.1b.

This illusion effect is well known by the ballet dancers and can be observed in movements such as grand jeté (Laws & Harvey, 1994). Pelé hits the ball at a height of about 2.2 m and the speed of the ball after the kick is about 8.9 m/s or 32 km/h; although not a power shot, the kick is faster than if the player would have hit the ball with his head.
During any human movement in the air, although one can change the rotational inertia and angular velocity of each segment as well as of the entire body, the product of these two physical quantities, known as quantity of angular movement or angular momentum, does not change for the entire body due to a fundamental conservation law in mechanics: the angular momentum of a system is constant if the sum of the external torques acting on the system is zero. Pelé seems to violate this law in his bicycle: at the beginning, just after he looses contact with the ground, it seems his body is not rotating and just before the ball striking, his kicking leg presents a lot of angular movement. This apparent violation can be explained if we remember that what is unchanged is the product between angular velocity and rotational inertia and one must look at the angular momentum of all segments to visualize what is happening with the angular momentum of the entire body. 

Fig.1e shows the angular momentum of each leg and of the whole body. Although the kicking leg has a greater rotational speed, the other leg, rotating in the opposite direction with a lower speed, surprisingly mirrors the angular momentum of the kicking leg such that the sum of the two momentum remains constant during the movement. This happens because the kicking leg is moving closer to the whole body CG than the other leg (meaning a lower rotational inertia for the kicking leg). Fig.1e reveals the real scissors in the bicycle kick: the perfect symmetric angular momentum profiles of the legs. The net result during the entire movement in the air is the same: the total angular momentum is constant, with the exception when part of the momentum is transferred to the ball as indicated in Fig.1e. But how Pelé would know in which speed he should rotate his leg in such way to counter balance the angular momentum of the kicking leg without rotating the trunk? 

Figure 1. Analysis of a Pelé's bicycle kick. Main phases of the bicycle kick: the jumping (1), the scissors (2), and the ball striking (3) (a). Vertical position of the center of gravity, CG, of the whole body and only of the trunk (b). Angular position of the legs (c). Rotational inertia of the kicking leg (d). The angular momentum of the whole body and of each leg (e). The boxes show instants of almost no variation in the curves. See the video of Pelé's bicycle kick here.

Final Comments

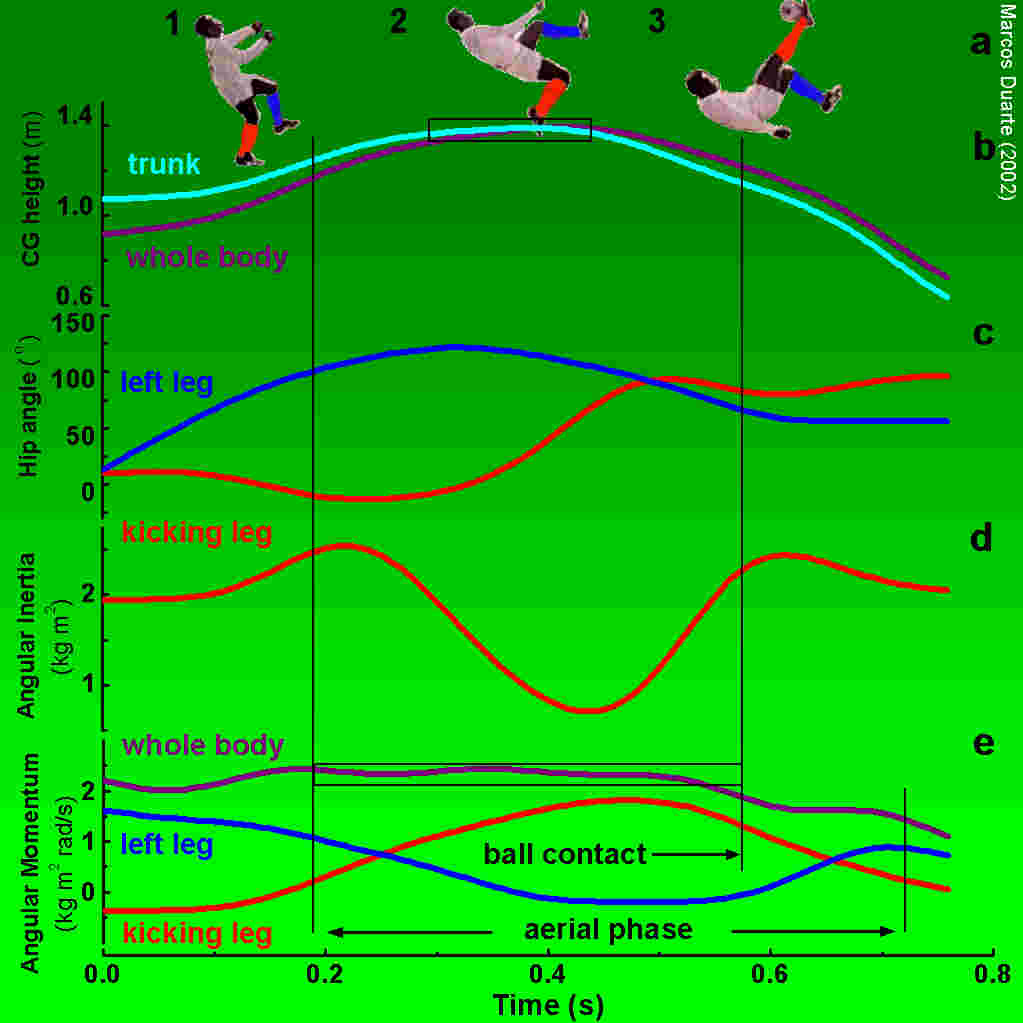
From the present analysis, two features can be pointed as distinctive of the perfect bicycle kick: first, one should be backwards and near parallel to the ground at the moment of the kick. Second and more exclusive, one must execute a particular movement with the legs, moving them in opposite directions before the kick like a scissors; or in physics language, the legs must have complementary angular momentum.

Any movement in nature, from particles to planets - and a bicycle kick by Pelé - cannot violate the fundamental principles of conservation of Mechanics. Saying that, it is not an attempt to belittle the splendor of such unique moment; rather it allows us to contemplate how science and art are partners in the same play.

But perhaps Pelé was more than we can understand...
In his final game in 1977, when Cosmos played against Santos at Giants Stadium in New York, it was raining after the game, and a witness explained: "God was crying".
References

Galeano, EH (1999) Football in Sun and Shadow. Verso Books. 
Laws, K & Harvey, C (1994) Physics, Dance, and the Pas de Deux. New York, Schirmer Books.
Oudejans, RRD et al. (2000) Errors in judging 'offside' in football. Nature 404, 33.
Zatsiorsky, VM (1998) Kinematics of Human Motion. Champaign, Human Kinetics.
Zatsiorsky, VM (2002) Kinetics of Human Motion. Champaign, Human Kinetics.

Links

Acknowledgements

This work was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo, FAPESP/Brazil. The author is thankful to Sandro F. Stolf for his technical help.